In this paper, knowledge of positive, negative, and fractional numbers, addition, subtraction, multiplication and division is assumed. Multiplication is represented by "*", division by "/", and priority by round brackets "()".
For example, if I have two chocolate bars, and I am considering the ethics of the situation, I might assign the value of the pleasure I get from eating a chocolate bar to the number "1". (This does not imply that "2" is the pleasure I get from eating both chocolate bars because, after the first, I've had my fill of chocolate for a while. [That is, the principle of Declining Marginal Utility applies.]) If we have an absolute and linear scale, "0" must be no pleasure at all, and "2" must be twice the pleasure I get from eating a chocolate bar, which is the same as the pleasure of two people each eating a chocolate bar, assuming that they like chocolate as much as me.
If we have a scale such that pleasures have a positive numerical value, then we can choose to represent pain and suffering on the same scale using negative numbers. For example, if I had a blister on my foot, I might think the pleasure from eating a chocolate bar isn't worth the suffering it would take to walk to the shop and buy one - in which case, I can say the value of the suffering caused by me walking on a blistered foot is less than (ie. more negative than) -1.
On some occasions, as I did above, we might immediately estimate the
value of a certain interest - combining the intensity and duration
factors automatically. At other times, we might consider them separately.
For example, in the ongoing chocolate bar example, whether or not it is
worth limping to the shops depends on how long it will take me to get
there (ie. for how long I'll have to suffer to get the chocolate bar).
We can model this mathematically using multiplication:
total suffering = average suffering per unit time * amount of time.
Notice by using the average suffering per unit time, I
have not committed myself to the assumption that the suffering is
constant - I may well find that suffering per unit time of walking on a
blistered foot depends on how much walking I've already done on it. I can
calculate the average amount of suffering per unit time over a given
period of time using:
average suffering per unit time = (suffering per unit time at the
beginning of the period + suffering per unit time at the end of the
period) / 2
as long as we assume a constant rate of change in the period.
If I
know the amount by which the suffering will increase in each unit time,
then:
suffering per unit time at the end of the period = suffering per unit
time at the start of the period + (rate of change of suffering * the
length of the period)
We usually consider that the actual outcome will be one of a possible set of (mutually exclusive) outcomes. If we represent the probability of the outcome occurring as a fraction (with 1 representing certainty and 0 representing impossibility, 0.5 representing a 50% ie. 1 in 2 chance etc) then the sum of the probabilities of the set must be 1 - if it was less than one, then either there is an alternative outcome we have not considered, or we have underestimated the probabilities of some of the outcomes - because we assume that one of the outcomes must actually occur (ie the probability of the result being one of the possible results is certainty, ie. 1). Notice that in this case the probability of A or B occurring is the probability of A occurring + the probability of B occurring.
When we deal with more complicated situations, ie. when there are secondary outcomes which become more or less likely depending on the initial outcome, then it may be helpful to draw the possibilities as a tree, where each branch represents an outcome, and the hierarchy indicates which possible outcomes follow from previous outcomes.

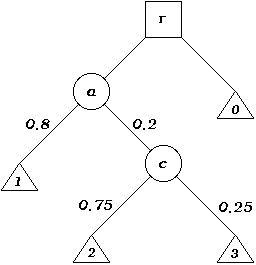
The tree consists of nodes and links. A node represents a situation, and a link indicates which situations can follow from which previous situations. The triangular nodes (called "payoff nodes") represent outcomes, and are numbered as above. The square node at the top (the root node "r") represents my position. It is square because it represents a choice I can make (it is a "decision node"): I can choose to do the act and go down the path to "a", or I can choose inaction and go down the other. The circular nodes represent situations which are resolved by chance, and are called "chance nodes". Chance node "a" represents the situation in which I choose to do the action; it leads to node "1" where I get away with it, and to node "c" where I get caught. The number by a link from a chance node indicates the (estimated) probability of that link being followed, given that we are already in the position above. (For example, it only makes sense to talk about the probability that I get caught in the case where I do choose to do the action - I don't get to position "a" until I've decided to act; and nodes "2" and "3" can only be reached from "c" - they can't try me if they don't catch me.)
The next step is to estimate the value for each situation represented by a payoff node. When estimating, we must consider intensity, duration, and extent of the interests involved (as compared to a baseline: usually inaction) - basically everything except certainty. I consider that, if I choose not to do the act, then everything continues as before: inaction has the value 0. I consider the value of my action (ignoring any cost to me) to be 1 [2], the value of being tried as -0.2 (due to the inconvenience etc), and the value of being tried, found guilty and punished as -2. [3] This gives the payoff values
The values are calculated from the bottom up. A decision node has the largest of the values of the nodes that follow from it - it is assumed we always choose to do what we think is most valuable. A chance node has an "expected" value [4] which is sum of the values of its sub-nodes, multiplied by their respective probabilities.
In this example, the expected value of "c" is:
(the probability of reaching node "2" * the value of node "2") + (the
probability of reaching node "3" * the value of node "3")
= (0.75 * -1) + (0.25 * 0.8)
= -0.75 + 0.2
= -0.55
The expected value of "a" can now be calculated as:
(the probability of reaching node "1" * the value of node "1") + (the
probability of reaching node "c" * the value of node "c")
= (0.8 * 1) + (0.2 * -0.55)
= 0.8 + (-0.11)
= 0.69
The next node up being a decision node, its value is simply the largest
of node "a" and node "0":
max(0.69, 0) = 0.69.
Since the expected value for node "a" is higher than that for node "0", and "a" represents what happens when I do this action, the tree therefore indicates that I should do the action (in preference to not doing it). If I could create a tree for a different course of action which (when using the same scale) returns a value greater than 0.69, then obviously I ought do that instead [5].
The procedure which has been described here, followed carefully, should avoid a number of the most common mistakes in moral mathematics.
I make no account of Mill's contribution: "quality". To the extent that the concept is intelligible, which isn't much, it seems entirely accountable with "intensity" and "fecundity". (I assume that there is a consensus on this - otherwise, we would hear people say such things as "I suffered a great deal, but it was only low quality suffering so it wasn't too bad" or "I had a lot of fun, but it gave only low quality happiness so it wasn't very good".) As an analogy to what I think Mill meant: we might assume that some pleasures were more valuable than others, in the same way that a given mass of gold might be more valuable than another given mass of gold of a different "quality" - perhaps the second mass is 9 carat, and the first is 18 or 24 carat. However, this doesn't really work because 1 unit of 9 carat gold isn't really 1 unit of gold - it is a nine "twenty-fourths" of a unit of gold, the rest of the mass being other metals. So under this interpretation quality and quantity (e.g. of real gold) cannot be distinguished in this way, which is why quality of pleasures can be accounted for by intensity.
Another possible interpretation comes from Mill's explanation of a higher quality pleasure being chosen in preference to a lower quality pleasure. This may mean simply that we like the idea of a certain means to happiness, more than we like the idea of some other means to happiness - we may like to think ourselves as someone who does the former but not the latter activity. But again on this interpretation Mill fails, since we are not here evaluating how much we like the idea of the experience of happiness gained in this way, but how much we like the experience of happiness itself. Any positive feelings associated with the idea of the thing are valuable (and evaluable) quite separately from the value of the thing itself.
2. ie. I'm setting the (arbitrary) units of the scale to be the same as the benefit of my action - all other values will be measured in comparison to this benefit.
3. Notice that the punishment is of uncertain type, duration etc, and thus disvalue, but that I have given it a definite value anyway: we can often continue analysing probabilities indefinitely, so at some point we simply estimate the value at a given level. If deeper analysis is required, this node should become a chance node with links to several other nodes, each representing different punishments.
4. The name "expected value" might be considered to be a mis-nomer: we do not actually expect this value to emerge - in fact is it generally impossible for it to do so (only the values of the payoff nodes can actually be achieved) - but the expected value is a kind of average of the possible values after taking into consideration their likelihood.
5. This is does not contradict the principle of utility, as Derek Parfit explains in his thoroughly recommended book "Reasons and Persons": consequentialists generally use and distinguish two different meanings of right and wrong, and ought and ought not. There is the sense, as in the principle of utility, that what we ought do (what it is right to do) is to maximize utility. However, we generally do not know what the consequences of our actions will be, so what we aim to do is act in such a way as to maximize expected utility. (As explained in the previous note, the expected value of an act rarely emerges - only the values of the payoff nodes can do so, assuming that the model is accurate). So there are two different questions here: 1. what is the best thing to do? 2. what seems to be, or is likely to be, the best thing to do? Unfortunately, we often cannot find the answer to the first question, which is why the second question needs answering.
The name given to these two senses - of something being really right, and of something being probably or seemingly right (i.e. what we have most reason to believe will be right) - is "objective" and "subjective" respectively; though this is perhaps unfortunate in that it suggests a relation to the question of whether ethics are objectively or only subjectively valid, and this is a separate issue entirely. Often, we hope, what is subjectively right is also objectively right - the two coincide. However it is obvious that this is not always the case: we can sometimes do the (objectively) wrong thing (i.e. most harmful) even though we had tried to do the right thing (we had weighed up the consequences, applying equal consideration etc). And vice-versa: someone might do something that appears to everyone (himself included) to be wrong (i.e. it is subjectively wrong), but actually has the best consequences.
Examples displaying the difference between the objective and subjective meanings include these:
